master-degree-notes/Concurrent Systems/notes/12 - Calculus of communicating system.md

• Up to now, we have considered non-deterministic processes

• Two main features are missing for modeling a concurrent system:

  • Simultaneous execution of processes
  • Inter-process interaction

• Solutions adopted:

  • Parallel composition, with interleaving semantics
  • Producer/consumer paradigm

[!note] Suggested reading https://en.wikipedia.org/wiki/Calculus_of_communicating_system

Given a set of names N (that denote events)

• a (\in N) denotes consumption of event a
• \bar{a} (for a \in N) denotes production of event a
• a and \bar{a} are complementary actions: they let two parallel processes synchronize on the event a

When two processes synchronize, an external observer has no way of understanding what is happening in the system

• synchronization is not observable from the outside; it produces a special ‘silent’ action, that we denote with τ The set of actions we shall consider is: N \cup \bar{N} \cup \{\tau\}

It is also useful to force some processes of the system to synchronize between them (without the possibility of showing to the outside some actions)

The restriction operator P\a restricts the scope of name a to process P (a is visible only from within P)

This is similar to local variables in a procedure of an imperative program

The set of CCS processes is defined by the following grammar: $$P::=\sum_{i \in I} \alpha {i}.P{i} \space |\space A(a_{1}\dots a _{n})\space|\space P|Q \space | \space P\setminus a$$ Dove:

• \alpha _{i}.P_{i}: the process P_{i} can perform the action a and continue as the process P_{i}
• A(a_{1}\dots a_{n}) parametric call to a process
• P|Q parallel composition: P and Q are in a concurrent execution and can communicate to each-other
• P\setminus a as described before, is the process P without a (the action is hidden / visible only internally by P)

Recap:

• P ⟶ᵃ P' means: Process P can perform action a and become P'
• α is an action: input (a), output (ā), or internal (τ)
• {a₁/x₁, ..., aₙ/xₙ} is a substitution (used in process definitions with parameters)

📜 Inference rules

1. Choice (Summation Rule)

{\sum_{i \in I} \alpha_i . P_i \xrightarrow{\alpha_j} P_j} \quad \text{for all } j \in I

A process that has multiple options (α₁.P₁ + α₂.P₂ + ...) can non-deterministically choose any one of them.

2. Process Definition (Call/Expansion)

\frac{P\{a_1/x_1, \dots, a_n/x_n\} \xrightarrow{\alpha} P'}{A(a_1, \dots, a_n) \xrightarrow{\alpha} P'} \quad A(x_1, \dots, x_n) \triangleq P

If a process A(x₁...xₙ) is defined as P, then invoking A(a₁...aₙ) behaves like P with the arguments substituted.

3. Restriction (Hiding)

\frac{P \xrightarrow{\alpha} P'}{P \setminus a \xrightarrow{\alpha} P' \setminus a} \quad \text{if } \alpha \notin \{a, \bar{a}\}

If process P can do action α and it’s not the hidden action (a or ā), then P \ a can also do it, and the resulting process remains restricted.

4. Parallel Composition – Independent Actions

There are three rules here for different situations in P₁ | P₂.

a. Left process makes a move:

\frac{P_1 \xrightarrow{\alpha} P_1'}{P_1 \mid P_2 \xrightarrow{\alpha} P_1' \mid P_2}

If P₁ makes a move alone, the parallel composition can reflect it.

b. Right process makes a move:

\frac{P_2 \xrightarrow{\alpha} P_2'}{P_1 \mid P_2 \xrightarrow{\alpha} P_1 \mid P_2'}

Symmetrical to the previous: P₂ makes the move.

c. Synchronization rule (communication):

\frac{P_1 \xrightarrow{a} P_1' \quad P_2 \xrightarrow{\bar{a}} P_2'}{P_1 \mid P_2 \xrightarrow{\tau} P_1' \mid P_2'}

If one process can send (a) and the other can receive (ā), they synchronize, and the result is an internal (τ) action. This models communication.

🧠 Summary Table:

Rule Type	Description
Choice	Select one summand to act
Process Call	Expand definition by substituting parameters
Restriction	Only allows transitions not involving the restricted action
Parallel (independent)	A single component acts, the other stays the same
Parallel (sync)	Two components synchronize to produce τ

Example

Example, but explained

📘 Definitions

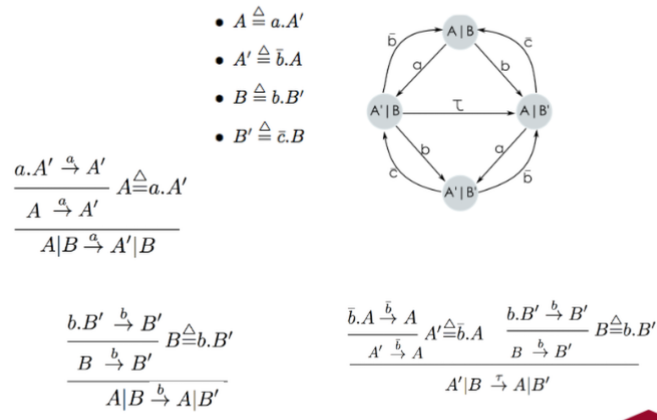
We start with the following process definitions:

• A \triangleq a.A'
• A' \triangleq \bar{b}.A
• B \triangleq b.B'
• B' \triangleq \bar{c}.B

Our initial process is: A \mid B

▶️ Step 1: Transition from A

From the definition:

• A \triangleq a.A'
  • So we can do: A \xrightarrow{a} A' (A consumes a and becomes A')

Using the parallel rule for the left-hand side:

\frac{A \xrightarrow{a} A'}{A \mid B \xrightarrow{a} A' \mid B}

✅ First transition: A \mid B \xrightarrow{a} A' \mid B

▶️ Step 2: Synchronization: \bar{b} and b

We now have:

• Left process: A' \triangleq \bar{b}.A
• Right process: B \triangleq b.B'

From this, we can do:

• A' \xrightarrow{\bar{b}} A
• B \xrightarrow{b} B'

These actions complement each other, so we can apply the synchronization rule:

\frac{A' \xrightarrow{\bar{b}} A \quad B \xrightarrow{b} B'}{A' \mid B \xrightarrow{\tau} A \mid B'}

✅ Second transition:

A' \mid B \xrightarrow{\tau} A \mid B'

▶️ Step 3: Transition from B'

From the definition:

• B' \triangleq \bar{c}.B
  • So: B' \xrightarrow{\bar{c}} B

Now use the right parallel rule:

\frac{B' \xrightarrow{\bar{c}} B}{A \mid B' \xrightarrow{\bar{c}} A \mid B}

✅ Third transition:

A \mid B' \xrightarrow{\bar{c}} A \mid B

Synchronization

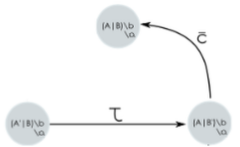
In the image above, we can observe a τ-transition due to synchronization between two complementary actions, in fact:

• A' produces b and becomes A
• B consumes b and becomes B'

Since \bar{b} and b are complementary actions, they can synchronize, resulting in a silent action \tau (synchronization rule):

\frac{A' \xrightarrow{\bar{b}} A \quad B \xrightarrow{b} B'}{A' \mid B \xrightarrow{\tau} A \mid B'}

LTS and parallelism

In the construction of the LTS we loose the consciousness of the parallel

• it is indeed possible, by having the new set of actions, to obtain the previous LTS through the syntax we considered last class.

The usefulness of the parallel is two-fold:

• it is the fundamental operator in concurrency theory
• it allows for a compact and intuitive writing of processes.

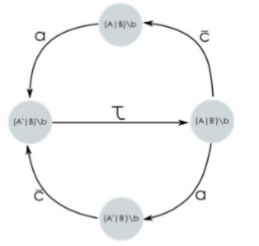
Restriction

What if we restrict on b?

Example 1:

since a is not in \{b, \bar{b}\}, we will see the transitions: \frac{\frac{\frac{a.A' \xrightarrow{a} A' \quad A \triangleq a.A'}{A \xrightarrow{a} A'}} {{A \mid B \xrightarrow{a} A' \mid B}}a \not \in {b, \bar{b}}}{{(A \mid B) \setminus b \xrightarrow{a} (A' \mid B) \setminus b}}

Split in separate peaces for better readability: $$\frac{a.A' \xrightarrow{a} A' \quad A \triangleq a.A'}{A \xrightarrow{a} A'} \quad \frac{A \xrightarrow{a} A'}{A \mid B \xrightarrow{a} A' \mid B} \quad \frac{A \mid B \xrightarrow{a} A' \mid B \quad a \notin {b, \bar{b}}}{(A \mid B) \setminus b \xrightarrow{a} (A' \mid B) \setminus b}

Example 2:

since b is in \{b, \bar{b}\}, we will NOT see the transitions: $$\frac{\frac{\frac{b.B' \xrightarrow{b} B' \quad B \triangleq b.B'}{B \xrightarrow{b} B'}} {{A \mid B \xrightarrow{b} A \mid B'}}b \in {b, \bar{b}}}{{(A \mid B) \setminus b}} This time I won't split it in separate pieces since I don't feel like doing it, just buy glasses.

So... What if we restrict on b?

• The effect of the restriction on b is that we have deleted the transitions involving b (hide all transitions labelled with b and \bar{b}).

• Notice that the τ, even if it has been generated by synchronizing on b, it is still present after applying the restriction on b!

  • the purpose of the τ is exactly to signal that a synchronization has happened but to hide the event on which the involved processed synchronized.

• In general, it is possible that whole states disappear upon restriction of some names: this would be the case, e.g., if we consider the LTS arising from (A’ | B)\setminus a,b (restricting on both a and b):