master-degree-notes/Concurrent Systems/notes/14 Checking bisimilarity, an inference system.md

We shall only consider finite processes (processes without recursive definitions)

• a limited handling of recursion is possible
• deciding bisimilarity for general processes is undecidable

Inference system = axioms + inference rules

• soundness: whatever I infer is correct (i.e., bisimiar)
• completeness: whatever is bisimilar, it can be inferred

Axioms & Rules for Strong Bisimilarity

just what we've seen so far, literally.

quite obvious.

basically we can let the left or the right process evolve, leaving the other unchanged, or they can synchronize. So we remove the parallel by just adding all the possible cases.

• if a process does not perform any action, a restriction won't do anything
• restriction is distributive
• if the process does not do the restricted action, the restriction won't do anything
  • what if we restrict on the actual action?
    • well, then the process becomes 0

• if P = P \land P = Q => Q = P (it's transitive :o)
• the same happens with contexts

Soundness theorem: \vdash P=Q \implies P \sim Q

Proof: If \vdash LHS=RHS, we need to consider the relation \{ LHS,RHS \} \cup Id and prove it's a bisimulation (spoiler: it is).

Since bisimilarity is an equivalence and a congruence, the inference rules holds.

[!def] Standard form P is in standard form if and only if P \triangleq \sum_{i}\alpha_{i}P_{i} and \forall_{i}P_{i} is in standard form.

Lemma: \forall P \space \exists \space P' in standard form such that \vdash P = P' Proof: by induction on the structure of P.

Base case: P \triangleq 0. It suffices to consider P' \triangleq 0 and conclude reflexivity. Inductive step: we have to consider three cases.

1. P \triangleq P_{1}|P_{2}. By induction, we have that \exists P_{1}',P_{2}' in standard form such that \vdash P_{1}=P_{1}' and P_{2}=P_{2}'.

   By context closure, \vdash P_{1}|P_{2}=P_{1}'|P_{2} and \vdash P_{1}'|P_{2}=P_{1}'|P_{2}'. Now we apply the axioms for parallel, until we remove all the occurrences of "|":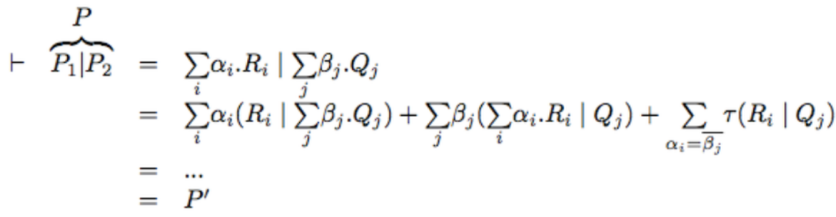 and eventually we find P' which is literally the standard form of P_{1}|P_{2}.

2. P \triangleq \sum_{i \in I}\alpha_{i}P_{i}. By induction \forall P_{i} \exists P_{i}' in a standard form s.t. \vdash P_{1}=P_{1}' Let's now consider a context: \alpha_{1}.☐ + \sum_{i \in I}\alpha_{i}P_{i} Now we fill the hole (er bucio) with P_1 and remove 1 from the set I (basically we pull it out from the summation): \alpha_{1}.P_{1} + \sum_{i \in I\setminus \{ 1 \}}\alpha_{i}P_{i} Now we replace P_1 with P_{1}' and obtain: =\alpha_{1}.P_{1}' + \sum_{i \in I\setminus \{ 1 \}}\alpha_{i}P_{i} imagine doing this until you pulled everything out... Standard form!

Axioms & Rules for Weak Bisimilarity

Completeness theorem: P \sim Q \implies \vdash P=Q

It's true.

Example

A server for exchanging messages, in its minimal version, receives a request for sending messages and delivers the confirmation of the reception

Specification: Spec \triangleq send.\overline{rcv} The behavior of such a server can be implemented by three processes in parallel:

• one handles the button for sending
• another one effectively sends the message (through the restricted action put) and waits for the signal of message reception (through the restricted action go)
• the last one gives back to the user the outcome of the sending

S \triangleq send.\overline{put} \quad M \triangleq put.\overline{go} \quad R \triangleq go.\overline{rcv}

Impl \triangleq (S|M|R)\setminus\{put, go\}

exercise: prove the weak bisimilarity

Let us consider the parallel of processes M and R, by using the axiom for parallel, we have \vdash M|R=put.(\overline{go}|R)+go.(M|\overline{rcv}) By using the same axiom to the parallel of the three processes, we obtain

\vdash S|(M|R)=send.(\overline{put}|(M|R))+put.(\overline{go}|R|S)+go.(\overline{rcv}|S|M)

By restricting put and go, and by using the second axiom for restriction, we have that:

We now apply the third axiom for restriction to the three summands: