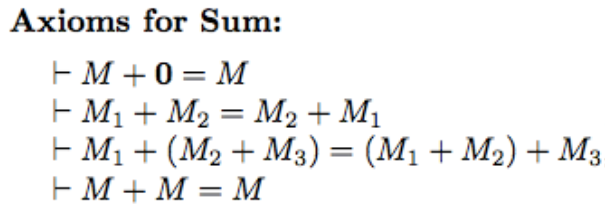1.3 KiB
1.3 KiB
We shall only consider finite processes (processes without recursive definitions)
- a limited handling of recursion is possible
- deciding bisimilarity for general processes is undecidable
Inference system = axioms + inference rules
- soundness: whatever I infer is correct (i.e., bisimiar)
- completeness: whatever is bisimilar, it can be inferred
Axioms & Rules for Strong Bisimilarity
quite obvious.
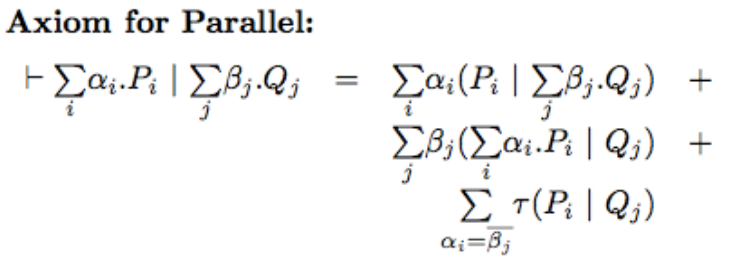basically we can let the left or the right process evolve, leaving the other unchanged, or they can synchronize.
- if a process does not perform any action, a restriction won't do anything
- ...
P is in standard form if and only if P \triangleq \sum_{i}\alpha_{i}P_{i} and \forall_{i}P_{i} is in standard form.
Lemma: $\forall P \exists P'$* in standard form such that \vdash P = P'
Proof: by induction on the structure of P.
Base case: P \triangleq 0. It suffices to consider P' \triangleq 0 and conclude reflexivity.
Inductive step: we have to consider three cases.
